Our dedication to Racial Equality and Social Justice (RESJ) spans decades. Learn more about our RESJ Initiative
An Irrational Man
Most everybody has heard of the Pythagorean Theorem. Pythagoras was a philosopher and mathematician of the sixth century B.C. E. with many followers, who were called the Pythagoreans. They believed in the transmigration of souls and lived according to strict rules of conduct. They were also the first to believe that nature could be described and understood with numbers, which is pretty much what science believes today, over 2500 years later. They also believed that all numbers could be expressed as rational numbers, or ratios of whole numbers. We now know that this is not true, there are real numbers that cannot be expressed this way, the so-called irrational numbers. Ironically enough, it is believed that the first person to discover this was Hippasus, himself a Pythagorean. The other Pythagoreans regarded this as heresy, and when Hippasus announced that he was going to reveal his discovery to the outside world, he “accidentally” drowned at sea, or so the story goes.
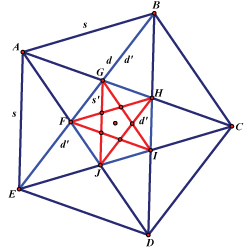
Historians conjecture that Hippasus was trying to determine the ratio of the length of a side to the length of a diagonal in the regular pentagon. If you take a regular pentagon and draw its diagonals you get the so-called mystic pentagram, which at the time was the symbol of the Pythagoreans. The diagram below shows a regular polygon with diagonals drawn to produce two mystic pentagrams, one in blue and one in red: The outer blue pentagon has side length s and diagonal length d. It forms an inner regular pentagon with side length s' and diagonal length d'. We could continue this process, drawing diagonals and forming inner regular pentagons as many times as we want. The ratio that Hippasus was looking for was d/s, which is the same as d'/s'. Now suppose the ratio d/s could be expressed as a/b, where a and b are whole numbers. Then scaling the diagram so that d = a, we have s = b. In other words, by choosing an appropriate unit, we can assume that s and d are whole numbers.
From the geometric properties of the diagram, Hippasus derived the relationships between s, d, s' and d'. This isn’t easy, but we have done it as a class project....

